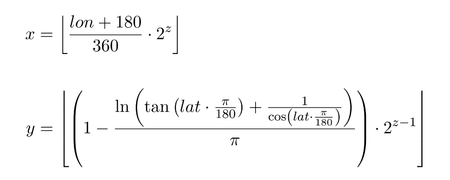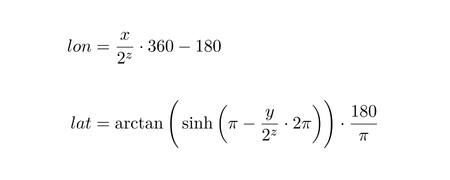FR:Repérage des carreaux de carte glissante
Cet article décrit les conventions de nommage et de coordonnées, utilisées pour le repérage des carreaux qui pavent les fonds de carte glissante tels qu›ils sont rendus dans les principales applications et éditeurs OSM, notamment sur le site web principal.
Niveaux de zoom
| Niveau de zoom | Description |
|---|---|
| 0 | 1 seul pavé couvre l’ensemble du monde (à l’exception des calottes voisines des pôles géographiques) |
| 1 | 2 × 2 pavés |
| 2 | 4 × 4 pavés |
| n | 2n × 2n pavés |
| 17 | Zoom maximum pour Osmarender |
| 18 | Zoom maximum pour Mapnik (sur le serveur OSM) ; certains serveurs peuvent zoomer encore au delà en produisant des pavés à la demande. |
x et y
- x va de 0 (le bord gauche est à la longitude 180° Ouest) jusqu'à 2zoom -1 (le bord droit est à la longitude 180° Est)
- y va de 0 (le bord supérieur est à la latitude 85,0511° Nord) jusqu'à 2zoom -1 (le coin inférieur est à la latitude 85,0511° Sud) dans une projection Mercator
85,0511 est la valeur en degrés de l’angle plan retournée par la formule arctan(sinh(pi)). En utilisant cette limite, la carte dans son ensemble (en excluant les zones polaires au delà de ces latitudes) devient un (très large) carré. Voir aussi l’anomalie d'Osmarender. Il n'est pas possible dans cette projection de visualiser jusqu'aux pôles car la carte entière deviendrait une bande verticale comprenant un nombre infini de carreaux dans les deux directions nord et sud (avec des valeurs non nulles de y).
Pour le niveau de zoom le plus faible (zoom = 1), x et y sont tous les deux invariablement à 0 (il n'y a qu'un seul carreau à ce niveau), qui correspond à la position géographique 0°N 0°E au centre de ce carreau (sur l'équateur et le méridien de référence géographique, ce point étant dans l'Océan Atlantique dans le Golfe de Guinée, à l'ouest de Saõ Tomé-et-Principe et au sud du Ghana).
Cependant les carreaux sont des images de 256 pixels de côté (numérotés de 0 à 255 de haut en bas ou de gauche à droite). Pour convertir des coordonnées d'un pixel pointé en coordonnées géographiques, il faut d'abord repérer la position d'affichage du centre du carreau pointé afin d'obtenir des coordonnées relatives (de -127,5 à +127,5) du pixel pointé sur ce carreau, puis diviser ces coordonnées par 256 pour les ajouter ensuite aux coordonnées entières x et y du carreau pointé : les valeurs de x et y ci-dessous ne sont donc pas nécessairement entières, sauf au centre de chaque carreau.
De plus il faut faire attention au fait que l'affichage d'un carreau complet d'image peut utiliser plus oumoins de pixels physiques que de pixels définis dans l'image servie (selon la résolution du dispositif d'affichage et son propre dispositif de zoom).
Toute application peut également afficher un carreau qui n'est pas encore disponible à un niveau de zoom donné, en agrandissant ou réduisant un l'image d'un carreau déjà servie pour un autre niveau de zoom : des facteurs d'ajustement proportionnels (non nécessairement identiques entre les deux coordonnées si le dispositif d'affichage a des pixels non carrés, par exemple avec une résolution verticale différente de la résolution horizontale) devront être appliqués pour convertir les coordonnées d'affichage d'un pixel pointé dans le carreau rendu, en coordonnées virtuelles en pixels (de 0 à 255) dans l'image carrée calculée et servie de ce carreau.
Projection
- Le système de projection utilisé est celui de Mercator.
- Les valeurs x sont la division de l’équateur en n unités égales de longitude (partant de 0 depuis le bord droit du côté est l'antiméridien et allant vers l'est jusqu'au le bord gauche du côté ouest de l'antiméridien)
- Les angles ±85.0511° de la projection sont les limites de la carte sur l'axe vertical Y.
- Les valeurs y sont la division de l'axe Y de la carte en n unités égales (partant de 0 sur depuis le bord inférieur jusqu'en haut)
Mathématiquement, quand lat et lon sont en degrés décimaux et z est le niveau de zoom :
En Perl:
use Math::Trig;
sub getTileNumber {
my ($lat,$lon,$z) = @_;
my $xtile = int(($lon + 180) / 360 * 2 ** $z);
my $ytile = int((1 - log(tan($lat * pi / 180) + sec($lat * pi / 180)) / pi) / 2 * 2 ** $z);
return( ($xtile, $ytile) );
}
En Actionscript 1 ou Javascript:
function long2tileX(lon, zoom) {
return Math.floor(
(lon + 180) / 360
* Math.pow(2, zoom)
);
}
function lat2tileY(lat, zoom) {
return Math.floor(
(1 - Math.log(Math.tan(lat * Math.PI / 180) + 1 / Math.cos(lat * Math.PI / 180)) / Math.PI) / 2
* Math.pow(2, zoom)
);
}
En Java :
public class slippytest {
public static String getTileNumber(final double lat, final double lon, final int zoom) {
int xtile = (int)Math.floor(
(lon + 180) / 360
* (1 << zoom));
int ytile = (int)Math.floor(
(1 - Math.log(Math.tan(lat * Math.PI / 180) + 1 / Math.cos(lat * Math.PI / 180)) / Math.PI) / 2
* (1 << zoom));
return ("" + zoom + "/" + xtile + "/" + ytile);
}
public static void main(String[] args) {
int zoom = 10;
double lat = 47.968056d;
double lon = 7.909167d;
System.out.println("http://tile.openstreetmap.org/" + getTileNumber(lat, lon, zoom) + ".png");
}
}
En VB.NET :
Private Function CalcTileXY(ByVal lat As Single, ByVal lon As Single, ByVal zoom As Long) As Point
CalcTileXY.X = CLng(Math.Floor( _
(lon + 180) / 360 _
* 2 ^ zoom))
CalcTileXY.Y = CLng(Math.Floor( _
(1 - Math.Log(Math.Tan(lat * Math.PI / 180) + 1 / Math.Cos(lat * Math.PI / 180)) / Math.PI) / 2 _
* 2 ^ zoom))
End Function
Conversion inverse des pavés Mercator aux coordonnées géographiques
Mathématiquement la conversion inverse est:
En Perl :
sub ProjectF {
my $Lat = shift;
$Lat = deg2rad($Lat);
my $Y = log(tan($Lat) + (1 / cos($Lat)));
return( $Y );
}
sub ProjectMercToLat($){
my $MercY = shift();
return( atan(sinh($MercY)) * 180 / pi );
}
sub Project {
my ($X, $Y, $Zoom) = @_;
my $Unit = 1 / (2 ** $Zoom);
my $relY1 = $Y * $Unit;
my $relY2 = $relY1 + $Unit;
my $LimitY = ProjectF(85.0511);
my $RangeY = 2 * $LimitY;
$relY1 = $LimitY - $RangeY * $relY1;
$relY2 = $LimitY - $RangeY * $relY2;
my $Lat1 = ProjectMercToLat($relY1);
my $Lat2 = ProjectMercToLat($relY2);
$Unit = 360 / (2 ** $Zoom);
my $Long1 = -180 + $X * $Unit;
return( ($Lat2, $Long1, $Lat1, $Long1 + $Unit) ); # S, W, N, E
}
En Actionscript 1 ou Javascript :
function tileX2long(x, zoom) {
return x / Math.pow(2, zoom) * 360 - 180; /* bord ouest */
}
function tileY2lat(y, zoom) {
var n = (1 - y / Math.pow(2, zoom) * 2) * Math.PI;
return Math.atan((Math.exp(n) - Math.exp(-n)) / 2) * 180 / Math.PI; /* bord nord */
}
Pavés
- Les pavés sont des images carrées de 256 × 256 pixels au format PNG.
- Chaque niveau de zoom est un répertoire, chaque colonne est un sous-répertoire, et chaque pavé dans cette colonne est un fichier.
- Le format du nom de fichier (fin de l'URL) est
URL de base/zoom/x/y.png
La carte glissante compte sur ce schéma d'URL, ainsi tous les URLs du serveur de pavés sont identiques. Par exemple :
|
http://tile.openstreetmap.org/8/127/85.png
|
|
http://tah.openstreetmap.org/Tiles/tile.php/8/127/85.png
|
|
http://osm-tah-cache.firefishy.com/~ojw/Tiles/tile.php/8/127/85.png
|
Pavés de zoom inférieur
| Ouest | → Est | |
|---|---|---|
| Nord | (2x, 2y) | (2x+1, 2y) |
| ↓ Sud |
(2x, 2y+1) | (2x+1, 2y+1) |
Si vous regardez le pavé (x, y) et que vous voulez obtenir aux pavés couvrant la même région géographique au niveau de zoom immédiatement supérieur, les sous-pavés sont (dans le système de coordonnés du niveau de zoom suivant) positionnés et numérotés comme dans le schéma ci-contre.
De la même manière, reculer d’un niveau de zoom se fait en divisant par deux x et y (du niveau de zoom précédent).
Attention : si la ligne verticale médiane a une longitude facile a calculer (il s'agit de la simple moyenne arithmétique des longitudes des deux bords à droite et à gauche du pavé à subdiviser), ce n'est pas le cas pour la ligne horizontale médiane car l'axe Y dans cette projection n'obéit pas exactement à une progression linéaire en fonction de la latitude (si vous regardez un pavé entièrement dans l'hémisphère nord, la latitude médiane est située légèrement en dessous de la ligne médiane horizontale de subdivision des pavés. Pour calculer la latitude correspondant à la ligne de découpe des pavés, utilisez les formules ci-dessus. En revanche pour le passage du niveau de zoom 0 (un seul pavé couvrant toute la carte) au zoom 1, le calcul est simple car cette ligne médiane horizontale correspond exactement à l'équateur (latitude 0) : à tous les niveaux de zoom, il y a autant de pavés dans l'hémisphère nord que dans l'hémisphère sud.
Cette remarque s'applique également pour convertir en coordonnées géographiques la position d'un pixel pointé dans un pavé, particulièrement pour les faibles niveaux de zoom où la non linéarité de l'axe y n'est pas négligeable lorsque le pavé recouvre verticalement un grand écart de latitudes (la précision désirée des coordonnées géographiques dans OSM est au maximum décimétrique, ce qui correspond à moins d'un cent-millième de degré pour les latitudes).
Outils
- X,Y <-> lat/long (page actuellement en erreur, mais le source Perl est accessible : source)
References
- http://econym.org.uk/gmap/reference.htm
- "Google Map" projection, see Spatialreference.org [1]