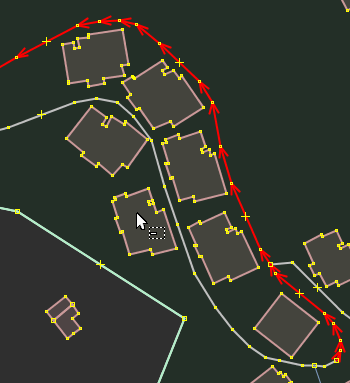
JOSM/Plugins/RemoveRedundantPoints
Why using the RemoveRedundantPoints plugin?
The purpose of the plugin is, given a curve composed of line segments, to find a similar curve with fewer points. The algorithm defines 'dissimilar' based on the maximum distance between the original curve and the simplified curve. The simplified curve consists of a subset of the points that defined the original curve.
Caveats
Be careful when using this plugin:
- it may also keep only segments which will underably cut through other features (such as roads passing through houses or cutting rivers without any bridge), notably if they are not loaded in the editor;
- there's no maximum bound for absolute angular change of directions, so it may severely affect the curve by keeping only irrealistic sharp angles (for now there's no angular threshold to preserve a minimum flatness, and no attempt to move the preserved nodes in order to better fit the initial curve);
- some deleted nodes may have useful tags (such as traffic signs) that should have been preserved (and these nodes should eventually not moved at all such as reference survey points), or could be useful members of relations to preserve in order to not break their semantics: this plugin does not check any tag or membership of nodes it removes from ways, this could leave orphan nodes outside any way and with meaningful tags that make no sense outside the way they were initially part of their geometry.
So please use conservative values for the threshold, not below the typical half-width and natural irregularities of features represented by flattened curves (such as highways, railways, waterways, riverbanks, lakes/ponds, coastlines, beaches, retaining walls, barriers along highways or cliffs): it may be useful, prior to use this tool, to split the way to smaller sections, on which you'll apply this simplification, before eventually joining it again.
Mathematical bases(Douglas–Peucker algorithm)
The starting curve is an ordered set of points or lines and the distance dimension threshold > 0.
The algorithm recursively divides the line. Initially it is given all the points between the first and last point. It automatically marks the first and last point to be kept. It then finds the point that is furthest from the line segment with the first and last points as end points (this point is obviously furthest on the curve from the approximating line segment between the end points). If the point is closer than threshold to the line segment then any points not currently marked to be kept can be discarded without the simplified curve being worse than threshold.
If the point furthest from the line segment is greater than threshold from the approximation then that point must be kept. The algorithm recursively calls itself with the first point and the worst point and then with the worst point and the last point (which includes marking the worst point being marked as kept).
When the recursion is completed a new output curve can be generated consisting of all (and only) those points that have been marked as kept.
The implementation of this algorithm can be seen in the source code of the plugin.
Availability
The plugin should be available in your JOSM Plugins preference window under "RemoveRedundantPoints" or you can download it from [1].
Usage
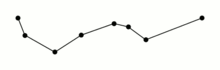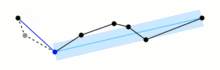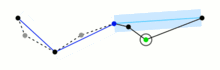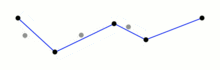
2. At the User Interface that are showing 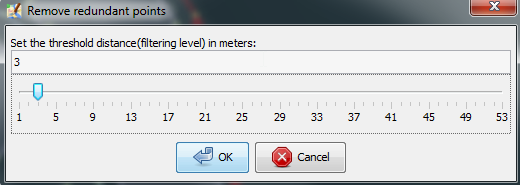 , user set the threshold distance.
, user set the threshold distance.
3. Way with part of nodes removed 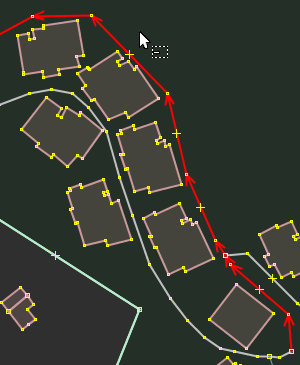
Note that example above is showing incorrect usage of this plugin - deleted points were useful to represent geometry of the way. Please avoid this type of edits.