Computing access restrictions
Problem
Given a specific highway and a specific transport mode, what is the corresponding access restriction? Basically we are supposed to "map what we see", that is road signs where there are any and "observe country specific defaults". However that approach needs considerable refinement:
- signs on roads/highways mean different things in different countries. So there needs to be a "translation mechanism" to translate "road signs/highway" into OSM restrictions
- implicit/default restrictions and interpretation are highly complex and may depend on country, landuse&ownership etc
- some type of highways like path/track (formal/informal) vs unpaved roads are vaguely defined
Example: suppose a specific highway=cycleway is tagged motor_vehicle=destination. How does it behave with respect to a motorcar? And to a horse?
The answer, whichever it is, must be computable by a routing software. Our aim is to provide a suitable algorithm everybody agrees upon.
A few tricky questions
A highway=cycleway is tagged access=destination. Does this imply:
- bicycle=destination, since access is more generic than bicycle, or
- bicycle=designated, since it's a cycleway?
- probably needs a per-country table translating road-signs into OSM restrictions
A highway=cycleway is tagged access=destination. Does this imply:
- motorcar=destination, since access is more generic than motorcar, or
- motorcar=no, since a cycleway implies access=no which in turn implies motorcar=no?
Parameters
What is on the ground
We are supposed to map road signs, i.e. what we see on the ground. However the full situations is slightly more complicated. There are
- road signs - with obviously country specific meaning)
- implicit restrictions, in the luckier cases those are well defined and nation wide, in the worse case those are the kind of restrictions like "except when there is a wetland nearby and bird XXX is nesting and the moon is 3/4 but not during Ramadan"
- country wide default restrictions tables were created with the idea to define the implicit restrictions but generally do not work because implicit restrictions are more complicated than what any table can express
The road signs and implicit restrictions need to be translated to OSM type access-restrictions. Currently this is mostly done by the mapper following a complicated set of local rules.
Transport mode tags
The set of transport mode tags: this set needs not be complete nor set in stone, and could evolve over time when new transport mode tags are created. Here is a partial list:
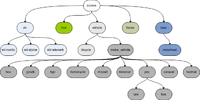
Transport mode hierarchy
We then need a relationship between the above tags, that is we need to state which tag is more generic and which one is more specific. Technically speaking, we want to arrange our transport mode tags in a tree structure, where the tree root is the most generic tag and tags get more specific as we move away from the root.
This tree is derived from Key:access and is not complete: some transport modes are missing. Other trees are possible: each country, for instance, can have its country-specific hierarchy. For instance, horses are considered vehicles in some countries.
Highway-specific defaults
As third and last parameter, we need default access restrictions for every highway type: that is, we need a set of defaults for highway=cycleway, another one for highway=motorway, etc.
Such defaults should be in the most generic form (see here to get an idea of most general unifiers), that is a default which states access=no must be preferred to a default which explicitly states motorcar=no, motorcycle=no and so on for each transport mode tag.
For instance, the default for highway=cycleway could be access=no and bicycle=designated.
Each country could have its own country-specific defaults. The current defaults are documented here.
Algorithm
Input:
- a specific highway with zero or more explicit access restrictions;
- a specific transport mode (e.g. bicycle, foot, motorcar etc.)
Output:
- an access restriction (e.g. no, yes, destination, private etc.)
Steps:
- Label the "access" node of the tree as "unknown", which is the default access restriction.
- Take the highway-specific defaults and use them to label the access mode tree. For instance, if the highway is a highway=cycleway and its defaults are access=no, bicycle=designated, the resulting tree will be:
- node access is labelled no
- node bicycle is labelled designated
- all other nodes are unlabelled
- Take the explicit access restrictions and apply them to the tree in the same vein; if a node is already labelled, overwrite its previous label with the new one. For instance, if the only explicit access restriction is motor_vehicle=destination the resulting tree after this second step will be:
- node access is labelled no
- node bicycle is labelled designated
- node motor_vehicle is labelled destination
- all other nodes are unlabelled
- Take the transport mode given as input and look it up in the tree: the output is the node label (if the node itself is labelled) or the label of its closest labelled ancestor. For instance, if the transport mode given as input is motorcar:
- node motorcar is not labelled, so look at its parent motor_vehicle;
- node motor_vehicle is labelled destination, so the algorithm output is destination.
Remarks
Adapting the algorithm to a specific country
The algorithm parameters are:
- the set of transport mode tags
- the transport mode hierarchy
- the highway-specific defaults
Therefore the algorithm is still valid if:
- new transport mode tags are introduced/old ones are removed
- country-specific rules modify the transport mode hierarchy (for instance stating that horses are / are not a vehicle)
- country-specific rules modify the highway-specific defaults (for instance stating that mopeds are allowed on a cycleway)
Therefore if you want to adapt this algorithm to your country:
- do not alter the algorithm itself
- document your country-specific rules (transport mode hierarchy and highway-specific defaults)
Trees vs DAGs
The algorithm supposes that the set of transport mode tags can be arranged into a tree: each tag (apart from the root node) has one and only one parent. If one wanted to model more complex relationships (where e.g. motorboat has two parents: boat and motor_vehicle) one needs to introduce directed acyclic graphs (DAGs) instead of trees. However this generalization could lead to the notorious multiple-inheritance problem of object-oriented languages.
- This provides an insight into the future creation of new transport mode tags: when new tags are introduced, one must be careful that no tag has more than one parent.
A few worked-out examples
Suppose that highway=cycleway's defaults are access=no, bicycle=designated. Suppose that a given cycleway is tagged foot=designated. This means that:
- The access restriction for bicycle and foot is designated.
- The access restriction for anything else is no.
Suppose that highway=cycleway's defaults are access=no, bicycle=designated. Suppose that a given cycleway is tagged bicycle=permissive. This means that:
- The access restriction for bicycle is permissive.
- The access restriction for anything else is no.
Suppose that highway=cycleway's defaults are access=no, bicycle=designated. Suppose that a given cycleway is tagged access=destination. This means that:
- The access restriction for bicycle is designated.
- The access restriction for anything else is destination.
Suppose that highway=cycleway's defaults are access=no, bicycle=designated. Suppose that a given cycleway is tagged access=permissive, vehicle=no. This means that:
- The access restriction for bicycle is designated.
- The access restriction for all other vehicles is no (this is true e.g. for motorcars).
- The access restriction for anything which is not a vehicle (e.g. foot) is permissive.