Generalization

The idea of Cartographic Generalization is well described in Wikipedia [1]. One important aspect of generalization is the accuracy and number of details of collected data.

The generalization of curves in map is the answer to the question: how detailed existing way or outline should be mapped?

The answer is different in different situations. On the one hand OSM says: we map the reality, on the other hand using too many nodes is not helpful - thousands of nodes is too much to represent a single roundabout.

General discussion

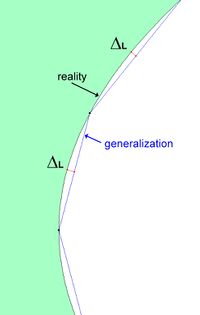
Let´s look at this sketch:

According to different size of Delta L the results would be more or less generalized.

Looking upon the elliptical shape:

one might see: with the same Delta L the distance between nodes is as longer as more "straight" the way to be digitized is.

Looking at the real shape:

The lenght of one segment would be ca. 130,9 cm.

explains the difference between "good" and "bad" generalization. "Bad" has the same distance between nodes and wasted map:

"Good" generalization considers differences in curvature of digitized shape:

How small the Delta L value is, is the decision of the local community.

Practical examples

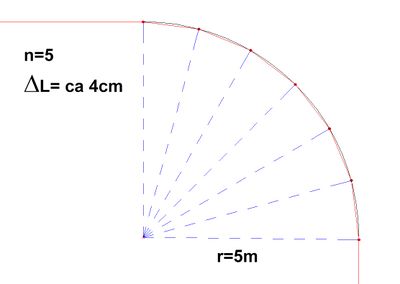
Streets in western countries have often rounded boudaries in crossing area. Common radius for rounding is around 5 meter by crossing angle of 90°.

The curve may be generalized by use of some points. Given that the radius of such curve have exactly 5 meter and maper divide this in:

12 segments so is the Delta L= 2cm.

Divided in

7 segments - Delta L= 3 cm

Divided in

6 segments - Delta L= ca. 4 cm

See:

The lenght of one segment would be aroud 131 cm. This seems to be ok. No higher detail level is needed.

Usecase JOSM PlugIn Fast draw

Parameters of PlugIn Fast draw:

- Epsilon multiplier=1.1

- Starting Epsilon=1

- Max points count per 1 km=300

- Enter key mode=Siplify with initial epsilon.

provides a good resolution for most of naturar, irregular areas like e.g. forests, rivers and lakes.