Altitude
Altimetry is the process of obtaining the height above a fixed level. This article will describe how to perform altimetry and how to enter the data into OSM.
Background
Shape of the Earth
Before any location can be described on the Earth, it is necessary to define the planet's shape. The shape of the Earth is generally approximated with an ellipsoid, a slightly flattened sphere. The exact dimensions and shapes of the ellipsoid vary among standards, but the WGS-84 reference ellipsoid can be considered typical.
Elevation

Every measurement is done around a reference point, and elevation is no exception. Now given a three-dimensional point in space and a reference ellipsoid, it is simple to calculate the height above the surface of the ellipsoid (shown as h in the image). However, such a result would not be very useful, mainly because the Earth's gravity is not uniform.
Traditionally, elevation and altitude both refers to a height above sea level (H), where the mean sea level (MSL) value is based on some local measurements near the shore and extrapolated inland with gravity. In modern times, it is common to replace the value with the geoid, an imaginary surface derived from measurements on the Earth's gravity. The geoid surface very closely matches the mean sea level, but factors like tide and ocean currents will produce some difference.
There are multiple models describing the MSL and the geoid. MSL models are generally local, while the geoid covers the entire world. The MSL and geoid surfaces are themselves described using the ellipsoidal height (hQG).
Types of height
While American measurements generally follow the geoid, resulting in a orthometric height, many countries in Europe use the easier-to-measure normal height with a quasigeoid reference. The quasigeoid closely approximates the geoid, and for the purpose of OSM any difference in concept is irrelevant.
In OSM
The OSM Data Model stores the 2D position (latitude and longitude) of points, and elevation is just an "afterthought" stored in the tag system under the ele=* and its subkeys. The following keys are recommended:
ele=*– Used to store the elevation relative to the EGM96 geoidele:wgs84=*– Used to store the elevation relative to the WGS84 ellipsoid
Elevations relative to other systems can be marked up using ele:xyz=####.##, where xyz is the name of the different reference system. The page on ele=* has more information on the list of reference systems you may encounter.
Height measurement in OSM

accuracy of 1 mm bolt
top

Elevation in OSM is always based on a reference level and the measured difference in height.
Heights are only useful if:
- The reference level is exact
- The height difference is exact
- The reference system of the reference altitude is known, and is converted into the reference system of OSM.
The cartographer must therefore know, which reference level, which Geoid and which Reference ellipsoid it references, when he makes his measurements. And he needs to know how to convert this reference frame to the reference system of OSM.
Reference height
Reference height is a precisely measured height, for example, a control point in a triangulation, or any derivative Survey marker. You can query reference heights from the local administration (Building Authority) or check with the local surveying office. Reference heights are usually marked with a wall stud (MB) or a level mark (HM). The accuracy is 0.1 to 100 mm.
In Germany, reference heights are defined in order steps 1 to 5 and with height stabilities 'a' (good) to 'c' (poor).
Conversion to WGS-84
The height inquired from the Building Authority must be converted into WGS-84 before it can be used for OSM. This is also true for all other elevation data from any source:
The prerequisite is that the frame of reference for the height indicated on the table is known. For Switzerland, one can assume that "m.ü.M." is equivalent to the LN-02 used in Switzerland. In (Western) Germany, one can assume that for the amount indicated on boards that existed before 1990 uses NN (or DHHN-12) (for newer tablets this is unclear, because it is often only copied from the old). For official heights, please ask the Office to which the claim relates for a reference system.
Conversion for Germany
- Ask the surveyor's office which reference system the claim relates to
- conversion of normal height into ellipsoidal height (Germany)
explanation of the conversion Form - in
ele:...=*Enter the reference system and the original elevation from the source - in
ele:wgs84=*enter the converted result in WGS-84
Height difference
Starting with the point of reference height, the height difference measured by an altimeter is used and added to the reference height:
- desired height = height + reference height difference
Producing a EGM96 value
The WGS-84 ellipsoidal height is nice, but it does not make much sense in real life. It must be converted to EGM96 before it can go into the ele=* tag.
- Look up the EGM96 geoid height at the point using https://geographiclib.sourceforge.io/cgi-bin/GeoidEval.
- Calculate the EGM96 elevation by subtracting the geoid height from your WGS-84 ellipsoidal height.
- Put the EGM96 elevation in the ele tag.
(The EGM96 has been replaced by a higher-quality EGM2008, but OSM is yet to catch up.)
Barometric altimeter
The barometric altimeter actually measures air pressure. Since the air pressure decreases with increasing altitude, it can directly indicate the height, when calibrated properly.
Accuracy
The accuracy of barometric altimeters in the measurement of height differences lies between 2 and 10 metres, provided the devices are temperature stabilized and the air pressure does not change due to weather change. Exact devices are available from 30 euros up.
For non-temperature-stabilized units, the temperature must be kept constant around +-5 degrees. (don't take it out of the pocket in the cold mountain air, nor hold it once in the warm hand and once with gloves on)
- Meteorological pressure fluctuations must be compensated for by all means
Pressure fluctuations are difficult to detect (for non-meteorologists) because it cannot be distinguished, whether the air pressure has changed meteorologically, or by changing the height.
Measurement Guide
- Query official measurement point and underlying reference system (reference point)
- Convert the height of the reference point into WGS-84
- Calibrate the barometric altimeter at the reference point. Use the height already converted into WGS-84 for this
- Read and note the height difference at the point to be measured
- Every three hours re-calibrate against the known value (at the Plunger) calculated in WGS-84 level.
- for each pointː Add height WGS-84 reference point and altitude difference:
Attentionː Don't perform barometric altitude measurements on days with front passages passing (storms, rising or falling barometer).
GPS altimetry
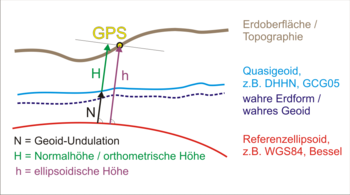
The GPS device is located at the yellow dot "GPS", somewhere on the earth's surface. The GPS device 'knows' where it is currently located (x / y / z-coordinate). It knows the calculated value of the WGS-84 ellipsoid. The device also knows some reference points of a (quasi)geoid between which it interpolates and thus calculates the difference between the reference ellipsoid and the (quasi)geoid (undulation). The computational cost of this is very large and therefore almost always an average value is used instead. For Germany, this is 47,5 metres.
The device calculates the ellipsoidal height from the coordinate and the WGS-84 ellipsoid. From that height and the approximate (quasi)geoid it calculates the approximate elevation and displays it. Note that:
- Given how approximate the undulation is, such altitudes are almost always imprecise, so you should start by getting the ellipsoidal height.
- The GPS technology itself can produce large deviations in height on the order of 40 meters unrelated to the undulation used. The measurement is therefore unusable without averaging.
Professional devices can, however, with appropriate corrections, measure and calculate heights exactly in the millimetre range.
NMEA data
In the NMEA data you see the following fields:
$ GPGGA, time, latitude, longitude, quality, satellite number, accuracy, 115.3, M, 47.5 M
│ │ │
│ │ └> geoid-height
│ └> Elevation
└> GGA key
Each device uses different data for the Quasigeoid internally, sometimes even every firmware version of the device uses different computational rules. Some GPS devices use plain 47.5 metres, but this height is not correct. Others for example print -67.8 metres. If we add the 115.3 metres from the NMEA Data, we obtain the 47.5 metres.
Ellipsoidal height
The ellipsoidal height is the most accurate measurement. This is calculated directly from the satellite data. But it will not be displayed directly, but is the sum of the quasigeoid height and the normal amount contained in NMEA. The value of the ellipsoidal height should always be used for the OSM database, because all other heights can be derived from them and any elevation models be calculated.
from:
Ellipsoidal height = Normal height + quasigeoid
results:
Normal height 115.3 m Display Quasigeoid height 47.5 m internally, inaccurate ellipsoidal height 162.8 m Originally calculated
The value you get here is the ellipsoidal height suitable for the ele:wgs84=* tag. For conversion to EGM96, see #Producing a EGM96 value above.
Cartography

Representation
Height differences are displayed using contour lines. For better visual identification of the mountains and valleys, slopes are often shaded.
Cartographic representation of strong gradients (cliff escarpment, Cliff, ravine, deep valley) requires special map symbols. This is not feasible with contour lines even with a small contour interval of 10 metres.
In OSM renders
Elevation tagged on points is not rendered into any OSM maps. A topographic map requires a continuous area coverage, something the node-based tagging can't do. Such coverage is generally provided by so-called digital elevation models.
The OpenCycleMap rendering of OSM generates contour lines using an abridged version of the SRTM data from Viewfinder Panoramas. SRTM is an 2001 Space Shuttle mission that figures out the shape of the ground using radars.