Isochrone
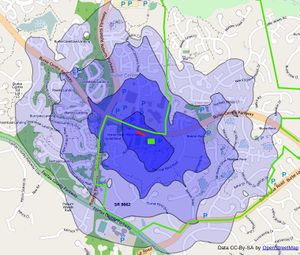
An isochrone is an isoline for travel time, that is a curve of equal travel time. Closely related is isodistance, which is a curve of equal travel distance. Typically these are based upon following transportation routes such as public transit, roadways, or foot paths rather than using a simple circle (a.k.a. buffer of a point, "as the crow flies" distance). This article will use the term isochrones, however any weighting factor can be used such as distance, or even a combination such as safety and time.
Applications
| Name, link | Genre | Covered region | Languages | Description | Free materials | Image |
|---|---|---|---|---|---|---|
| CommuteTimeMap [1] | Worldwide | English | Allows you to build and visualize isochrones worldwide. | maybe | ||
| finderful.com | Isochrones, routing, housing | Australia | English | Find homes in a certain travel time "radius". Shows isochrone on map. Australia only. | No. | |
| Geoapify | Maps, geocoding, routing, isolines | Worldwide | English, German | Isochrones and reachability maps for different transportation modes: walk, bicycle, auto, transit. | Yes | |
| Iso4App [2] | Worldwide | English | Isochrones based on GTFS data. | maybe | ||
| Safe Routes to School Mapping Toolkit | Worldwide | English | working to create travel distance/time web app for pedestrians and bicyclists using OSM data (source code available) | maybe | ||
| TargomoAPI | Routing, isochrones, points/statistics reachability | Worldwide | English, German | Targomo offers routing-based analysis tools - isochrone polygons, points-of-interest, A-B routing, reachability, fleet management, statistics reachability for the following transportation modes: walk, bike, car, transit. | Yes | |
| TravelTime platform | Isochrones, routing, geocoding, distance matrix | English | Create isochrone shapes with an API or export to KML, get journey times from 1-100,000 points of interest in 1 request. Routing and geocoding also available. Available as a plugin for QGIS and ArcGIS. | Yes. | ||
| Walkscore Travel Time API | United States | English, German | Uses GTFS and OSM data for maps of Seattle, San Francisco, and Washington DC. Built on the open source Graphserver library. (no source) | maybe | ||
| WNYC Transit Time | New York City | English, German | Public transit isochrones for New York City | maybe |
Software libraries
- GraphHopper [3][4] can be used to calculate a detailed time information for every point within a certain time or distance reach.
- GRASS v.net.iso module
- OSRM Isochrone Generate drivetime isochrones from OSM using OSRM.
- pgRouting driving_distance() function
- pysochrone is a Python script and simple web interface for computing and displaying isochrones from an OGR-supported data source (e.g. PostGIS)
- Valhalla isochrone service
APIs for developers
- Geoapify Isochrone API - API service to build isochrones for drive, truck, bicycle, walk and transit modes. Worldwide.
- GraphHopper Isochrone API
- Iso4App Isochrone/Isodistance map api service. Covered countries: Europe,Russian Federation, Ukraine, Lithuania, Latvia, Estonia, Belarus, North America, Central America, Australia-Oceania, South Africa. Javascript and Rest api available.
- Mapbox Isochrone API
- OpenRouteService Isochrones Service - uses OSM data and map, shows isochrones worldwide (no source code available)
- OpenTripPlanner - a development branch has work on an Analytics Extension, which currently provides isochrones based on the OSM network and GTFS data (source code available)
- TargomoAPI - Travel times, Routing, Points of Interests, Isochrones - developer tools to build state-of-the-art geospatial analytics applications, enhance location search, and personalize user experience
- TravelTime API creates isochrones for public transport, cycling, walking, driving and combined modes. Live across North America, Europe, Australia and other countries listed here.
Technical details
Creating an isochrone
Starting with a transportation network, such as OSM, we must create a shortest path tree (SPT) using something like Dijkstra's algorithm. This results in a set of points with associated travel times. This data isn't very meaningful by itself, but it can be transformed in several ways to create a useful result.
- Raw point layer - points can be drawn as circles (buffers) with the color indicating the distance, however if intersections aren't closely spaced the resulting render will imply certain regions aren't accessible even if they are.
- Convex hull - this is a polygon with the minimum area which surrounds all the points, however this will include areas which are unreachable
- Alpha shapes - similar to convex hull, however it allows for holes, so it is a better representation
- 2D interpolation - interpolating the points using something like natural neighbor produces smooth gradient-like results, however it is not the best representation since unreachable areas will likely be included
- Filled contours - taking points interpolated to a regular grid, contour lines are created for a finite number of values, such as 5 min, 10 min, etc; has same disadvantages as simple 2D interpolation but results are more easily interpreted
- Buffered roads - from the points extract the roads (edges) and buffer these, which produces a polygon that should fairly accurately represent the actual areas which are reachable; can take the intersection of filled contours and buffered roads to get the best of both worlds
For all of these methods it is best to interpolate along edges to ensure the maximum weight is represented (i.e. it is unlikely an intersection node will be at the exact max weight). Which method is chosen depends on the goals. For a pretty picture filled contours are likely the best choice.
Research
- Scientific Research with Isochrones at the Free University Bolzano/Bozen (including ISOGA demo)
- Scientific Research with Isochrones at the University of Innsbruck (including IsoMap demo) using OSM data. Multimodal isochrone computation is supported based on GTFS data.
- Calculating accessibility using open source software and open data - paper by McGurrin and Greczner, using OpenTripPlanner for travel time maps
See also
- Isoline
- Distance maps - this should likely be consolidated with this page